This article explains the Mundell-Tobin effect by showing the relationship between the ISLM and ADAS models. The Mundell-Tobin effect states that nominal interest rates may not rise 1:1 with price levels, as the Fisher effect states.
The Fisher effect derives from Fisher’s identity of i = r + π where i=nominal interest rates, r = real interest rates and π=inflation rate (i.e. rate of change in price levels). Fisher believed that if π rose by 1 then i must also rise by one.
Mundell-Tobin came along and said that this wasn’t the case, because they believed that r, the real interest rate, would fall if inflation rose, meaning the overall effect would be that i didn’t rise on a 1:1 basis with inflation. The reason, they said, that r falls is because higher inflation means people would rather save than hold money: if more people are saving money then the real interest rate falls. Ergo, inflation rises whilst r falls so i doesn’t rise at the same rate as inflation.
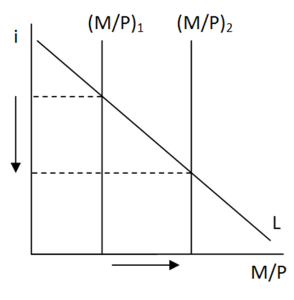
We use our ISLM and ADAS models to show this by examining an increase in the money supply. To analyse the increase in money supply we will first use the real money balance model:
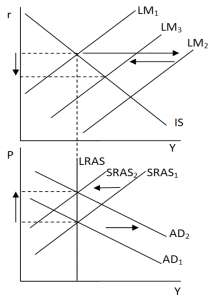
The increase in M shifted the M/P curve rightward so that the nominal interest rate falls. The effect of this in an ISLM setting is for the LM curve to shift rightwards. In an ADAS model aggregate demand would shift right. But this would mean that inflation is greater than expected inflation (assuming adaptive expectations) and so short run aggregate supply would eventually shift upwards (note, this may take a few periods of time as expectations take time to catch-up with reality, although I have shown this as a sudden movement), so that expected inflation=real inflation and we are operating again on the long run aggregate supply curve.
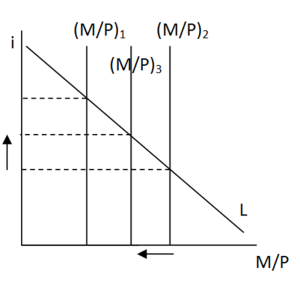
But you can see we now have higher inflation, so P has risen. This means that if we return to our real money balance diagram we would have to shift (M/P)2 left to (M/P)3 which would shift the LM curve leftwards. Now LM3 is between LM1 and LM2, but only because I have assumed that inflation is at a low level and so doesn’t entail a drastic response from the central bank to rise interest rates significantly.
Examination of our variables on these diagrams shows that inflation has risen – as expected – but that r has fallen (although not by as much as first expected due to the reinforcing mechanism which exists between the ISLM and ADAS models). Because r has fallen at the same time as inflation has risen it can’t be possible for i to rise at the same pace as inflation. Hence, we can conclude that the Fisher effect may not always hold as a useful rule of thumb and that sometimes the nominal interest rate will rise on a less than 1:1 basis with inflation; this is known as the Mundell-Tobin effect.