This post will review the econometric method of difference-in-discontinuities design, outlining the technical details, the strength and weaknesses, and provide an intuitive explanation for how this method can be used to identify causal effects of a treatment policy. In doing so, we will refer to its application in Ferguson and Kim (2023). Firstly, we outline the empirical question posed by Ferguson and Kim (2023) and discuss some potential ways of answering this question, to then motivate the use of the difference-in-discontinuities design approach.

Ferguson and Kim (2023) apply the difference-in-discontinuities technique to answer the question of whether a policy of decentralised agricultural production (called the Household Responsibility System or HRS) can causally explain the increase in agricultural yields seen in China in the late 1970s and 1980s. Existing literature suggests that the cause of China’s agricultural revolution – which enabled its industrial revolution and rapid economic growth, which led to a mass reduction in worldwide inequality and poverty as a result – was the HRS, yet much of these claims are built on non-causal studies (e.g. Lin, 1992; Li et al. 2016). This study instead applies the difference-in-discontinuities design method to answer this question and finds, contrary to the existing evidence, that HRS was not in fact responsible for the increase in agricultural yields. The true driver was instead likely to be the rebalancing of state prices for agricultural goods towards free-market-levels. In addition to taking a carefully identified causal approach, these authors also utilise satellite data to produce their measure of crop yield, given the widespread acknowledgement of the unreliability of official Chinese statistics. The key policy conclusion from this study is that there is no evidence that decentralisation of agricultural product resulted in higher production in China, as previously claimed.

Let us consider the most straightforward way of answering this research question based on the available data of agricultural yields (from satellite data) and provincial-level data on HRS adoption. We wish to estimate the effect that HRS adoption (independent variable) has on the agricultural yield (dependent variable) by province and time period. Note that treatment (HRS adoption > 50%) occurs at different points in time for different provinces, making it a staggered rollout. The simplest estimation method would be to compare treated provinces (those with high HRS adoption) with untreated provinces (those with low HRS adoption). If treated provinces have a higher agricultural yield than non-treated provinces, we might conclude that treatment increased agricultural yield. A simple regression analysis, estimating the following linear regression using ordinary least squares and treating observations as pooled, as below, would be the approach taken in this simple example (where i=province and t=year):

Yield_{i,t} = \alpha + \beta (Treatment_{i,t} = HRS>50\%) + \epsilon_{i,t}

A positive coefficient on beta would then indicate that treatment results in higher yields. However, this doesn’t account for the fact that treated provinces may have happened to have had high agricultural yields which did not change pre- and post-treatment. If there was no pre- and post-treatment change in agricultural yields for the treated units, then it is difficult to argue – based on a treatment vs non-treatment comparison alone – that treatment had any effect on yields.

A more sophisticated analysis would compare both differences between treated and untreated units and differences between treatment and non-treatment periods within province. This captures both across (provinces) and within (time) variation. Such a technique is known as difference-in-difference, or two-way fixed effects (TWFE) when applied in multiple-unit multiple-time-period framework. It can easily be implemented by defining a treatment variable equal to one in treated provinces in periods where HRS treatment is greater than 50%. OLS estimation can then be conducted by regressing the outcome variable (agricultural yields) on the dependent variable (treatment indicator) and controls for unit (province) and time-period (year). The appropriate regression equation would look like above but now include a province (i) and year (t) fixed effect:

Yield_{i,t} = \alpha_i + \gamma_t + \beta (Treatment_{i,t} = HRS>50\%) + \epsilon_{i,t}

A two-way fixed effects model would provide an unbiased estimate for the treatment effect under four assumptions: (i) parallel trends, (ii) no confounding policies, (iii) non-staggered treatment, or staggered treatment but homogeneous treatment effects across cohort group and (iv) exogeneity of treatment. The first assumption, parallel trends, states that prior to treatment, the treated unit and the control units must have the same trends. In this context, that means treated provinces must have had similar paths for agricultural yields as non-treated provinces, prior to treatment. Note, that this only requires similarity in trends not in value. This means that two provinces can have different levels of agricultural yield but their growth rate must be the same. If this condition holds, then it means that the treatment and control are similar enough for comparison between them to be valid. Then, we assume that in the absence of the treatment policy, the treatment and control group would have continued to follow the same path for the outcome variable. Any difference can thus be attributed to the policy. This assumption is shown graphically in the figure below.

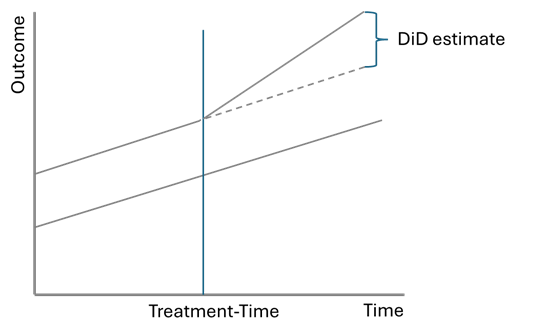
The second assumption, no confounding policies, simply means it must have been the case that no other policy which affected agricultural yields was implemented over the same period as the treatment being studied. If another policy occurred at the same time, then we won’t be able to distinguish between the effect of that policy and the effect of the policy we care about.

Our third assumption is that we either have non-staggered adoption of treatment or that if we have staggered adoption, we have homogeneity in the treatment effect across treatment cohort. This assumption is motivated by a recent literature which finds that with staggered treatment (and non-homogeneity in treatment effect), there is a negative weighting being applied due to a “forbidden comparison”, which renders the TWFE estimator biased (Callaway and Sant’Anna, 2021; Chaisemartin and D’Haultfoeuille, 2020; Goodman-Bacon, 2021; Roth et al., 2023). These forbidden comparisons occur because TWFE makes comparisons between (a) treated and not-yet-treated groups, (b) treated and never-treated groups, and (c) treated early and treated-late groups. The first two comparisons, (a) and (b) are called clean comparisons and are correct. However, the comparison in (c) can cause a problem in the presence of heterogeneous treatment effects, as we clearly wouldn’t be capturing an unbiased treatment effect. If we compare an early treated group – that is further along its treatment effect transition – with a newly treated group, then we are clearly going to estimate an incorrect treatment effect than when we compare a newly treated group with a never treated group.

If this assumption does not hold, then we need to take an approach which only compares the treatment group with “clean” controls. Such approaches include the Callaway-Sant’Anna estimator (Callaway and Sant’Anna, 2021), imputation methods (Gardner, 2021; Borusyak et al., 2023), stacked regressions (Cengiz et al., 2019; Freedman et al., 2023; Wing et al., 2024), or fully saturated treatment-cohort heterogeneity models (Wooldridge, 2021).

Finally, we require that the treatment itself is exogenous. In this application, the authors suspect that HRS adoption is in fact endogenous, as HRS adoption was not randomly allocated but was decided at the provincial level. It might be expected that provinces which have certain characteristics which could impact the outcome variable (e.g. poverty levels) are more/less likely to adopt the treatment policy. In this case, the treatment is endogenous and we do not estimate an unbiased estimate for the treatment effect. This then motivates the estimation strategy of difference-in-discontinuities, to overcome this endogeneity, which we turn to next before demonstrating how this was applied in the context of Ferguson and Kim (2023).

The difference-in-discontinuities approach combines a panel dataset with the regression discontinuity design (RDD) approach. RDD studies compare very similar units who are on an (exogenous) cut-off for being eligible to receive treatment. There is thus a discontinuity in treatment assignment, where treated and untreated units in a narrow bandwidth either side of this discontinuity should have similar unobservable characteristics and the effects of treatment can therefore be compared.

This exogenous cut-off could be a quantitative measure (e.g. Thistlewaite and Campbell, 1960; Bharadwaj et al., 2013), a time deadline (e.g. de Blasio et al., 2015) or a geographic boundary (as used in Ferguson and Kim, 2023). As an illustration, a typical RDD which uses a quantitative measure as the exogenous cut-off could be exam grades, where students who pass a grade threshold receive treatment into a university scholarship whilst those below the grade do not. We can then test the treatment of receiving the scholarship by comparing students who narrowly passed the exam versus those who narrowly failed. If we define “narrow” appropriately, then it is likely that students who narrowly failed are very similar in unobserved characteristics to those students who narrowly passed. We can thus compare those students and treat treatment status as exogenous. The RDD approach requires that there is no manipulation of treatment – for instance, teachers scoring students to ensure they get the scholarship – which can be tested by looking at bunching around the discontinuity (using a McCrary test). Such a condition ensures that students are truly comparable and can be thought of as akin to the parallel trends test in the difference-in-difference paradigm.

In the context of Ferguson and Kim (2023), the authors use farmer distance from the border as their measure of regression discontinuity and combine this with their panel dataset, taking fixed effects at the provincial level to eliminate unobserved provincial level characteristics which could affect treatment. In other words, the authors are concerned that they don’t want to just compare provinces which had high HRS adoption rates with those with low adoption rates, controlling for fixed effects and seeing the effect on agricultural yields, as they are concerned that HRS adoption is itself endogenously determined and that there might not be parallel trends between treated and untreated provinces.

To alleviate such concerns, they focus on a narrow geography (up to 50km) around the border. Here, we would expect farms to be of similar quality in terms of land quality and factors relevant for agriculture, such as crops grown. As the authors state: “assuming that all relevant factors other than treatment vary smoothly across the border, any discontinuities in outcomes observed at the border can be causally attributed to the treatment”. Hence, we should be convinced that parallel trends is likely to occur around the border area. Put differently, we would expect the land quality within a few miles of the border to be of a similar quality to the land quality a few miles the other side of the border. However, on one side of the border the policy of HRS is applied and on the other it is not. The only reason the HRS is applied on one side of this small area is due to historical accident and not because the culture or ideals of the people, or the quality of the land, differs across this border.

Whilst this condition is likely to satisfy the parallel trends assumption it raises another concern: the threat of spillover effects. If treatment results in improved outcomes, i.e. HRS adoption leads to increased agricultural yields, then we might expect these practices to spillover across the border. We can easily imagine that farmers on the non-treatment side of the border notice that their nearby neighbours are adopting a different agricultural practice and that it is reaping large rewards, so they decide to also adopt this agricultural practice. If spillover of treatment occurs, then we would clearly estimate a null effect of treatment. To elaborate, if our measure of treatment effect is comparing the treated border-region with the non-treated border-region, then in the presence of spillover effects, we would estimate a null (or close to zero) treatment effect. This is indeed the conclusion of Ferguson and Kim (2023), hence the need for them to convince us that spillover effects do not occur.

They do so by making two arguments: (1) migration is strictly controlled such that individuals on one side of the border couldn’t migrate to the other side of the border to take advantage of better outcomes in the presence of treatment effects, and (2) HRS was widely seen in Communist China as a capitalist threat to the established ideology prevalent in the country, therefore certain provinces were idealistically opposed to applying the treatment and therefore strongly resisted, and policed, any non-compliance. If these two conditions are to be believed, then it would satisfy the no spillover condition.

To further clarify the identification strategy we pose two questions: (a) if border regions do not suffer from spillover effects because residents cannot easily migrate, then how is it possible to assume that they have similar characteristics in terms of economic and political differences?, (b) why bother focusing on border regions – when fixed effects are being taken – and not simply the entire province? The answer to the first question is that this motivates the use of the difference part of differences-in-discontinuities design. By including fixed effects in addition to an RDD strategy, the authors are able to remove any time-invariant discontinuities, such as political and economic differences, along the border which may have presented a risk to identification. Hence, an RDD approach in itself would not be sufficient as an identification strategy but the difference-in-discontinuities design is required. The second question is more difficult to answer: why is a difference-in-difference approach at the provincial level not taken? This approach would remove any unobserved time-invariant differences between provinces and would allow the researchers to focus on the more homogeneous unit of a province, rather than the potential heterogeneous unit of a border area. The only sensible conclusion is that there may be concerns about time-variant unobserved differences at the provincial level which is solved by looking at the border. This could be, for instance, changes in agricultural usage or techniques over time at the provincial level which would not differ at the border area. Such an omitted variable could lead to endogeneity concerns if it were not controlled for through the RDD aspect of this identification strategy.

Moreover, a more concerning identification issue in the first identification strategy is that the authors are using a measure of treatment that a province is coded as treated if “the share of work teams in the province who have adopted HRS exceeds 50%”. It is not immediately clear that treatment will be uniformly distributed across province. In fact, we may expect treatment to be stronger in geographically central areas, where political ideology is stronger. If the border areas that are designated as treated have not in fact adopted HRS, then it is not surprising that a null effect is found in terms of treatment effect. This concern is not currently addressed by the authors but could be mitigated by evidence confirming that border regions were similar in their treatment status to the province as a whole.

Nonetheless, the authors additionally present a staggered difference-in-difference approach to confirm their findings. In this approach, the authors use a different dataset which shows treatment effects at the county-level and apply the two-way fixed effect whilst ensuring they only evaluate valid (and not forbidden) comparison groups. This increases confidence in their conclusion, and alleviates concern about the status of treatment coding discussed above, but suggests that earlier concerns of endogeneity of treatment – which motivated their use of a difference-in-discontinuities design – may not have been necessary.

Finally, the authors discuss the fact that there was only one other treatment effect that occurred in the Chinese agricultural policy landscape at a similar time – that of increasing procurement prices paid to farmers. This does not interfere with their causal estimates because it affects all provinces equally but may instead explain why other authors found a positive effect from HRS.

In conclusion, the two identification strategies utilised by the authors present a convincing argument that the null effect of treatment is indeed causally valid.

References

Bharadwaj, P., Løken, K.V. and Neilson, C., 2013. Early life health interventions and academic achievement. American Economic Review, 103(5), pp.1862-1891.

Borusyak, K., Jaravel, X. and Spiess, J., 2021. Revisiting event study designs: Robust and efficient estimation. arXiv preprint arXiv:2108.12419.

Callaway, B. and Sant’Anna, P.H., 2021. Difference-in-differences with multiple time periods. Journal of econometrics, 225(2), pp.200-230.

Cengiz, D., Dube, A., Lindner, A. and Zipperer, B., 2019. The effect of minimum wages on low-wage jobs. The Quarterly Journal of Economics, 134(3), pp.1405-1454.

De Blasio, G., Fantino, D. and Pellegrini, G., 2015. Evaluating the impact of innovation incentives: evidence from an unexpected shortage of funds. Industrial and Corporate Change, 24(6), pp.1285-1314.

De Chaisemartin, C. and d’Haultfoeuille, X., 2020. Two-way fixed effects estimators with heterogeneous treatment effects. American Economic Review, 110(9), pp.2964-2996.

Ferguson, J. and Kim, O., Reassessing China’s Rural Reforms: The View from Outer Space.

Freedman, S.M., Hollingsworth, A., Simon, K.I., Wing, C. and Yozwiak, M., 2023. Designing Difference in Difference Studies With Staggered Treatment Adoption: Key Concepts and Practical Guidelines (No. w31842). National Bureau of Economic Research.

Gardner, J., 2022. Two-stage differences in differences. arXiv preprint arXiv:2207.05943.

Goodman-Bacon, A., 2021. Difference-in-differences with variation in treatment timing. Journal of Econometrics, 225(2), pp.254-277.

Li, X., Liu, N., You, L., Ke, X., Liu, H., Huang, M. and Waddington, S.R., 2016. Patterns of cereal yield growth across China from 1980 to 2010 and their implications for food production and food security. PLoS One, 11(7), p.e0159061.

Lin, J.Y., 1992. Rural reforms and agricultural growth in China. The American economic review, pp.34-51.

Roth, J., Sant’Anna, P.H., Bilinski, A. and Poe, J., 2023. What’s trending in difference-in-differences? A synthesis of the recent econometrics literature. Journal of Econometrics.

Thistlethwaite, D.L. and Campbell, D.T., 1960. Regression-discontinuity analysis: An alternative to the ex post facto experiment. Journal of Educational psychology, 51(6), p.309.

Wing, C., Freedman, S. M. and Hollingsworth, A., 2024. Stacked Difference-in-Differences. NBER Working Paper 32054

Wooldridge, J.M., 2021. Two-way fixed effects, the two-way mundlak regression, and difference-in-differences estimators. Available at SSRN 3906345.